"The authors develop a method for analysis of time series generated by a class of complex processes. They identify the mechanism that causes information divergence at each level in a hierarchy of such processes."
Signatures of infinity: Nonergodicity and resource scaling in prediction, complexity, and learning
James P. Crutchfield and Sarah Marzen
Phys. Rev. E 91, 050106(R) (2015)

Abstract:
We introduce a simple analysis of the structural complexity of infinite-memory processes built from random samples of stationary, ergodic finite-memory component processes. Such processes are familiar from the well known multiarm Bandit problem. We contrast our analysis with computation-theoretic and statistical inference approaches to understanding their complexity. The result is an alternative view of the relationship between predictability, complexity, and learning that highlights the distinct ways in which informational and correlational divergences arise in complex ergodic and nonergodic processes. We draw out consequences for the resource divergences that delineate the structural hierarchy of ergodic processes and for processes that are themselves hierarchical.

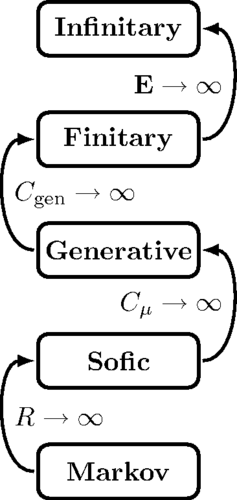
Figure 1

Prediction hierarchy for stationary ergodic processes: Each level describes a process class with finite informational quantities. A class above finitely models the processes in the class below. Classes are separated by divergence in the corresponding informational quantity. Moving up the hierarchy corresponds to it diverging. Example processes that are finitely presented at each level, but infinitely presented at the preceding lower level. Sofic: typical unifilar HMMs, e.g., the Even Process [1]; Generative: typical nonunifilar HMMs [32]; Finitary: typical infinite nonunifilar HMMs; Infinitary: highly atypical infinite HMMs with long-range memory, e.g., the ergodic construction in Ref. [4].
[http://dx.doi.org/10.1103/PhysRevE.91.050106]

Published: May 22, 2015, 3:33 pm