Remarkably robust and intelligent systems operate across the tremendous time and length scales of the natural world. At one extreme, nanoscale motor proteins shuttle nutrients along microtubule highways, adapting their loads to their host cell’s needs. At the other, an albatross on a 3,000-mile trek efficiently tracks and adaptively leverages wind fluctuations to radically reduce energy consumption as it circumnavigates an entire ocean without touching down. What is common in the behaviors spanning these immense scales is what Prof. Jim Crutchfield calls adaptive emergent computation.

The Army Research Office is supporting Prof. Jim Crutchfield to explore the fundamental principles of adaptive emergent computation and to experimentally demonstrate how thermodynamic forces can drive a system to be naturally programmable. The three-year $1.5 million project is an experimental collaboration with Prof. Michael Roukes (Kavli Nanoscience Institute, Caltech) to design arrays of nanoscale information-heat engines that exhibit emergent computation and with Prof. Erik Winfree (Computer Science, Caltech) to deploy his DNA computing technology to evolve emergent computation in chemical reactions.

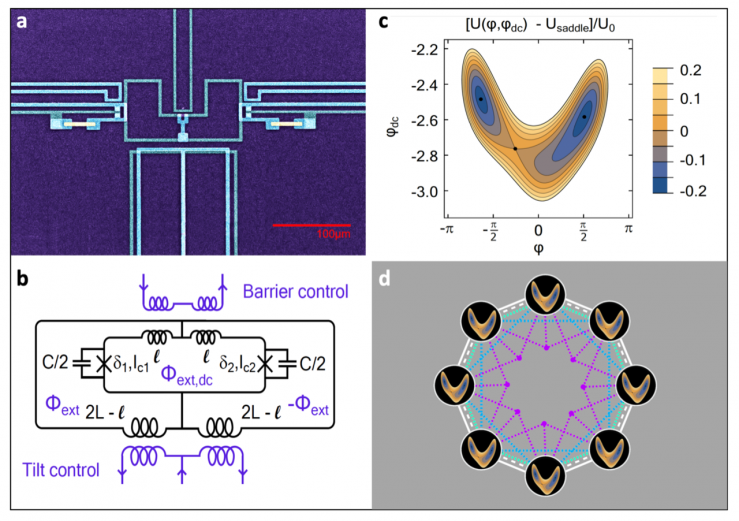
Gradiometric flux logic cell and its implementation into arrays, i.e., small networks, to enable our proposed studies. The magnetic fluxes threading the superconducting loops, though describing macroscopic phenomena, are true microscopic coordinates in the sense that other electronic degrees of freedom are frozen through condensation into a quantum-mechanical ground state. Static controls cause no dissipation on the device, as the magnetic fields are sourced with superconducting leads. (a) Device optical micrograph, realized as a two-layer superconducting circuit on an insulating silicon substrate. (b) Simplified circuit schematic of the information-bearing subsystem. We take the dynamical coordinates to be the total magnetic fluxes φ and φdc threading the loops. (c) Contour plot of the potential calculated for the component values of the studied device, and external bias fluxes—(φx,φ(x,dc)) = (−0.1018,−2.5887)—coinciding with the start of the bit erasure protocols that can be employed for proposed studies. Two local, metastable minima, and the unique saddle point are marked (black dots). (d) Example of ring-coupled topology, involving eight flux qubits. Higher-order interactions involving direct nearest-neighbor coupling and indirect next-nearest neighbor coupling are delineated.

Published: February 16, 2021, 10:21 am